Experimental implementation of arbitrary entangled operations

Entanglement is the key concept that makes quantum physics distinct from classical physics and plays an essential role in quantum information processing. As an entangled state cannot factor into a product of individual states, entangled operations cannot be represented by a product of individual operations but a coherent superposition of operations [1–5]. To date, superpositions of operators have been studied in both fundamental and practical aspects. Commutation relations for bosonic operators [6] and Pauli operators [7, 8] have been directly demonstrated experimentally using superpositions of operators, also Hamiltonian dynamics based on superposition of operations has been proposed theoretically [9]. Recently, it is reported that the superpositions of quantum operations can allow controlling the orders of quantum operations, which is not allowed in the traditional formalism of quantum physics [10–12]. This, so-called superposition of causal orders, is not only fundamentally interesting but also proven that it has practical applications in quantum information processing in the context of communication complexity [13, 14], witnessing causality [15, 16], quantum metrology [17], and transmission of quantum information [18].

However, so far research on superposition of quantum operations has been limited to superposition of single qubit gates in most cases, meaning that entanglement of operators has not been studied much yet. Most of the implementations of superposition of causal orders are relying on the interferometric scheme, however, in this case extension to an entangled operation is not straightforward since nonlocality should be involved. Extension to implementing an entangled operation is particularly important since a two-qubit entangled operation such as controlled-NOT (CNOT) gate can constitute the universal sets of quantum gates with single qubit gates [19–21]. Implementation of entangled operations for two-qubit systems can provide further advantages for practical quantum information processing, such as entanglement filter (EF) [22–24], entangling gate for universal quantum gate set [25], and entanglement generation for teleportation-based programmable quantum gate [7, 26–28]. It is also intriguing to explore entangled operations in even larger Hilbert spaces for investigating potential applications in quantum information processing.

In this letter, we propose and demonstrate a scheme for realizing an arbitrary entangled operation based on a coherent superposition of local operations. We first begin by introducing the concept of operator entanglement using an operator-Schmidt decomposition. We then present some intriguing and important operations that can be realized based on this scheme in two-qubit systems. Then, we describe our experimental demonstration of several two-qubit entangled operations in photonic systems and discuss our experimental results. Finally, we extend our scheme to the case of generalized entangled operations with N qubit systems and the Schmidt number M. We also present a practical scheme on implementing three-qubit entangled operations and introduce interesting three-qubit operations that can be implemented.

An operator ${\mathcal{O}}_{\text{AB}}$ acting on systems A and B can be written as

$$\begin{equation}{\mathcal{O}}_{\text{AB}}=\sum _{i}{c}_{i}{\mathcal{O}}_{\mathrm{A}}^{i}\otimes {\mathcal{O}}_{\mathrm{B}}^{i},\end{equation} \tag{ 1 }$$

where c_i ⩾ 0 and ${\mathcal{O}}_{\mathrm{A}}^{i}\enspace \left({\mathcal{O}}_{\mathrm{B}}^{i}\right)$ is orthonormal bases for a system A (B) [5]. Similar to the Schmidt representation of quantum states, equation (1) is the operator-Schmidt decomposition and the number of nonzero Schmidt coefficients c_i is defined as a Schmidt number [5]. If the Schmidt number of an operator ${\mathcal{O}}_{\text{AB}}$ is larger than one, ${\mathcal{O}}_{\text{AB}}$ is an entangled operator meaning that it can generate entanglement from separable states. It is clear that ${\mathcal{O}}_{\mathrm{A}}^{i}\otimes {\mathcal{O}}_{\mathrm{B}}^{i}$ with i = 1 could be prepared by local operations and classical communications between two distant systems A and B. However, in general, an operator having higher Schmidt number (i ⩾ 2) needs to implement a coherent superposition of operators ${\mathcal{O}}_{\mathrm{A}}^{i}\otimes {\mathcal{O}}_{\mathrm{B}}^{i}$ with different i [5].

Let us consider a simple case with the Schmidt number 2 and c₁ = c₂. Then,

$$\begin{align}\hfill {\mathcal{O}}_{\text{AB}}& =\frac{1}{\sqrt{2}}\left({\mathcal{O}}_{\mathrm{A}}^{1}\otimes {\mathcal{O}}_{\mathrm{B}}^{1}+{\mathcal{O}}_{\mathrm{A}}^{2}\otimes {\mathcal{O}}_{\mathrm{B}}^{2}\right)\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {A}_{2}\otimes {B}_{2}\right),\hfill \end{align} \tag{ 2 }$$

where ${\mathcal{O}}_{\mathrm{A}}^{1}={A}_{1}$, ${\mathcal{O}}_{\mathrm{A}}^{2}={A}_{2}$, ${\mathcal{O}}_{\mathrm{B}}^{1}={B}_{1}$, ${\mathcal{O}}_{\mathrm{B}}^{2}={\mathrm{e}}^{\mathrm{i}\phi }\enspace {B}_{2}$ and ϕ is the relative phase between A₁ ⊗ B₁ and A₂ ⊗ B₂. Note that the second line of equation (2) is not the Schmidt decomposition due to the complex number of coefficients, but it can explicitly show the relative phase ϕ between two superposed operations. In many cases, local operations are fixed but their relative phase can be varied. The entangled operation of equation (2) has a simple form, however, there are intriguing operations. When A₁ = B₁ = I, A₂ = B₂ = σ_x, equation (2) becomes

$$\begin{equation}\frac{1}{\sqrt{2}}\left(I\otimes I+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {\sigma }_{x}\otimes {\sigma }_{x}\right)=\frac{1}{\sqrt{2}}\left(\begin{matrix}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{e}}^{\mathrm{i}\phi }\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill {\mathrm{e}}^{\mathrm{i}\phi }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{e}}^{\mathrm{i}\phi }\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill {\mathrm{e}}^{\mathrm{i}\phi }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{matrix}\right),\end{equation} \tag{ 3 }$$

where I is an identity operation and σ_x, σ_y, and σ_z are Pauli operators. One can prepare maximally entangled states $\frac{1}{\sqrt{2}}\left(\left\vert 00\right\rangle +{\mathrm{e}}^{\mathrm{i}\phi }\left\vert 11\right\rangle \right)$ ($\frac{1}{\sqrt{2}}\left(\left\vert 01\right\rangle +{\mathrm{e}}^{\mathrm{i}\phi }\left\vert 10\right\rangle \right)$) from a separable input state $\left\vert 00\right\rangle$ ($\left\vert 01\right\rangle$).

When ${A}_{1}=\left\vert 0\right\rangle \left\langle 0\right\vert$, B₁ = I, ${A}_{2}=\left\vert 1\right\rangle \left\langle 1\right\vert$, and B₂ = U where U is a single qubit unitary operation, one can implement a controlled-unitary (CU) operation. In addition, by setting A₁ = B₁ = |0⟩⟨0|, A₂ = B₂ = |1⟩⟨1|, one can realize the EF which is a special non-unitary operation, and transmits the input states only when the incoming qubit states is either |0⟩|0⟩ or |1⟩|1⟩ [22–24].

However, it is difficult to implement an entangled operation of equation (2). Using an interferometer, it is possible to make a superposition of two different operators such as ${\mathcal{O}}_{\mathrm{A}}=1/\sqrt{2}\left({A}_{1}+{\mathrm{e}}^{\mathrm{i}{\phi }_{\text{A}}}\enspace {A}_{2}\right)$ [8]. However, when the system A and B use interferometers separately, what they prepare is $1/2\left({A}_{1}+{\mathrm{e}}^{\mathrm{i}{\phi }_{\text{A}}}\enspace {A}_{2}\right)\otimes \left({B}_{1}+{\mathrm{e}}^{\mathrm{i}{\phi }_{\text{B}}}\enspace {B}_{2}\right)$, which has clearly the Schmidt number 1. Note that if we apply A₁ and B₁ simultaneously to the system A and B with the half of the time and apply A₂ and B₂ with another half of the time, the prepared operation is an incoherent mixture of A₁ ⊗ B₁ and A₂ ⊗ B₂ rather than a coherent superposition of them.

Here, we propose a scheme for implementing an entangled operations using additional degree of freedom. The conceptual diagram of our scheme is shown in figure 1. For a two-qubit input state $\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle$, qubit an undergoes an operation A₁ or A₂ while qubit B undergoes an operation B₁ or B₂. In order to prepare an entangled operation, one needs to rule out A₁ ⊗ B₂ and A₂ ⊗ B₁ cases and the other two cases A₁ ⊗ B₁ and A₂ ⊗ B₂ should be coherently superposed. It is difficult to achieve these requirements, however, it is possible by using energy–time correlation of spontaneous parametric down conversion (SPDC) process. In experiment, the input state is encoded in a polarization of single photons. When a pair of photons are generated via SPDC process, the generated photon pairs have strong energy–time correlation. By exploiting this strong time correlation between two photons, one can prepare a coherent superposition of local operations, e.g., $\frac{1}{\sqrt{2}}\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {A}_{2}\otimes {B}_{2}\right)$ acting on polarization states of two-photons.

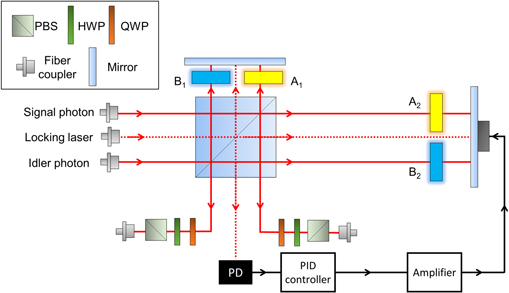
Zoom In Zoom Out Reset image size

The schematic of our experimental setup is shown in figure 2, which is based on Franson interferometer [29, 30]. We use a femtosecond pulsed laser operating at a center wavelength of 780 nm and a pulse period of 12.5 ns. The wavelength of the pump laser becomes 390 nm using a lithium triborate (LBO) crystal via second harmonic generation (SHG) process. Then, a pair of photons is generated via type-II SPDC process by pumping a 1 mm-thick beta-barium borate (BBO) crystal, and its polarization state is prepared in an arbitrary input state $\vert {\psi }_{\text{AB}}^{\text{in}}\rangle$ with a set of polarizer, half and quarter wave plates (WPs). Then, each photon is sent to an unbalanced Michelson interferometer (UMI) with different optical lengths of L₁ and L₂. The path length different L = L₂ − L₁ is 1.875 m corresponding to an half of the pulse period of the pump laser to ensure that the down-converted photons generated from consecutive pump pulses are temporally overlapped. Here we use an interference filter with 2 nm full-width at half maximum bandwidth, then the coherence length of each down-converted photon is around 300 μm. Hence, there is no first order interference at the output of UMI. In order to implement ${\mathcal{O}}_{\text{AB}}$ in equation (2), single qubit operations A₁ and A₂ (B₁ and B₂) are located in L₁ and L₂ arms of the UMI for a photon A (photon B), respectively. Note that a single qubit operation can be realized by linear optical elements such as WPs, polarizer (Pol.), and so on. The two-photon output states are analyzed by a set of WPs and Pol. using quantum state tomography (QST) and quantum process tomography (QPT).

Zoom In Zoom Out Reset image size

Let us describe the process of entangled operations of $\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {A}_{2}\otimes {B}_{2}\right)/\sqrt{2}$ for input state $\vert {\psi }_{\text{AB}}^{\text{in}}\rangle$ as following transformations:

$$\begin{align}\hfill \left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle \left\vert {t}_{\mathrm{A}}^{\text{in}}{t}_{\mathrm{B}}^{\text{in}}\right\rangle & \to \frac{1}{2}\left[\left({A}_{1}\otimes {B}_{1}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle \left\vert {t}_{\mathrm{A}}^{\mathrm{1}}{t}_{\mathrm{B}}^{\mathrm{1}}\right\rangle +\left({A}_{1}\otimes {B}_{2}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle \left\vert {t}_{\mathrm{A}}^{\mathrm{1}}{t}_{\mathrm{B}}^{\mathrm{2}}\right\rangle \right.\hfill \\ \hfill & \quad \left.+\left({A}_{2}\otimes {B}_{1}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle \left\vert {t}_{\mathrm{A}}^{\mathrm{2}}{t}_{\mathrm{B}}^{\mathrm{1}}\right\rangle +\left({A}_{2}\otimes {B}_{2}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle \left\vert {t}_{\mathrm{A}}^{\mathrm{2}}{t}_{\mathrm{B}}^{\mathrm{2}}\right\rangle \right]\hfill \\ \hfill & \to \frac{1}{2}\left[\left({A}_{1}\otimes {B}_{1}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle +\left({A}_{2}\otimes {B}_{2}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle \right].\hfill \end{align} \tag{ 4 }$$

The system and ancilla qubits are encoded, respectively, on the polarization, |ψ⟩, and time-bin modes |t⟩. After implemented prepared operations with experimental set-up as shown in figure 2, there are four possible output cases as second step of equation (4). Here |t¹⟩ and |t²⟩ refer to qubit arrived from short and long path of UMI, respectively. Then we can post-select output state as $\frac{1}{\sqrt{2}}\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {A}_{2}\otimes {B}_{2}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle$. Here, we used a measurement operator as $\vert {t}_{\text{A}}^{1}\rangle \langle {t}_{\text{B}}^{1}\vert +\vert {t}_{\text{A}}^{2}\rangle \langle {t}_{\text{B}}^{2}\vert$, which is implemented by set the coincidence window (we use 3 ns) smaller than the time difference between L₁ and L₂ (12.5 ns). Note that this is possible due to strong time correlation between temporally overlapped photon pairs using UMI which has path length difference corresponding to pulse period of photon pairs. Note that mixed states can be prepared by adjusting the path length difference L of UMI differently from an half of the pulse period of the pump laser, then it reduces the temporal overlap of the down-converted photons generated from consecutive pump laser pulses. The post-selected output state $\left\vert {\psi }_{\text{AB}}^{\text{out}}\right\rangle$ becomes $\frac{1}{\sqrt{2}}\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {A}_{2}\otimes {B}_{2}\right)\left\vert {\psi }_{\text{AB}}^{\text{in}}\right\rangle$ where ϕ is the sum of relative phase differences in each UMI (ϕ = ϕ_A + ϕ_B). In order to fix ϕ, we attached piezoelectric actuators on both mirrors in the short arms of the UMI and drive them using proportional integral derivative (PID) controllers to lock the relative phases ϕ_A and ϕ_B. Here, we can choose ϕ between 0 to 2π using a set of QWP, HWP, and QWP on the locking laser (780 nm pump laser). See appendix A for detailed information on the controllable phase-locking technique we use.

We demonstrated various entangled operations based on our experimental setup shown in figure 2. The first entangled operation we consider is ${\mathcal{O}}_{\text{AB}}\left(\phi \right)$ with A₁ = B₁ = σ_z and A₂ = B₂ = σ_x, i.e., ${\mathcal{O}}_{\text{AB}}\left(\phi \right)=\frac{1}{\sqrt{2}}\left({\sigma }_{z}\otimes {\sigma }_{z}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {\sigma }_{x}\otimes {\sigma }_{x}\right)$. ${\mathcal{O}}_{\text{AB}}\left(\phi \right)$ is able to generate entanglement since for a separable input state $\left\vert HH\right\rangle$, the output state is $\left\vert {\psi }_{\text{AB}}^{\text{out}}\right\rangle =\frac{1}{\sqrt{2}}\left(\vert HH\rangle +{\mathrm{e}}^{\mathrm{i}\phi }\vert VV\rangle \right)$, the maximally entangled states. We implemented ${\mathcal{O}}_{\text{AB}}\left(\phi \right)$ with ϕ = 0, π/2, π, and 3π/2 and performed QST measurement to each output states. The density matrices of the output states are reconstructed using maximum-likelihood method [31, 32] and the experimental results are shown in figure 3. As shown in figure 3, one can adjust the relative phase ϕ and the realized operation works well. Note that for the input state $\left\vert HV\right\rangle$, the output state becomes $\left\vert {\psi }_{\text{AB}}^{\text{out}}\right\rangle =\frac{1}{\sqrt{2}}\left(\vert HV\rangle -{\mathrm{e}}^{\mathrm{i}\phi }\vert VH\rangle \right)$. See appendix B for experimental results for the input state $\left\vert HV\right\rangle$.

Zoom In Zoom Out Reset image size

In order to show the quality of the implemented operation, we also performed QPT measurement. Figure 4 shows the experimentally reconstructed process matrices χ for entangled operations $\frac{1}{\sqrt{2}}\left({\sigma }_{z}\otimes {\sigma }_{z}+{\sigma }_{x}\otimes {\sigma }_{x}\right)$ and $\frac{1}{\sqrt{2}}\left(I\otimes I+i{\sigma }_{x}\otimes {\sigma }_{x}\right)$. The corresponding process fidelities F_χ are 0.760 ± 0.005 and 0.762 ± 0.006, respectively. Here we use ${F}_{\chi }={\left[\mathrm{Tr}\left(\sqrt{\sqrt{{\chi }_{\mathrm{exp}}}{\chi }_{\text{ideal}}\sqrt{{\chi }_{\mathrm{exp}}}}\right)\right]}^{2}$ where χ_ideal (χ_exp) is the process matrix of the ideal (experimentally realized) operation. Note that F_χ results are obtained by performing 100 Monte-Carlo simulations on the QPT measurement results and the errors on the process fidelities corresponds to one standard deviation. We also provide QPT results of $\frac{1}{\sqrt{2}}\left(I\otimes I-{\sigma }_{x}\otimes {\sigma }_{x}\right)$ operation in appendix B. We attribute the non-unity process fidelity to the imperfections of our experimental setup. First, due to imperfection of the optical components such as BS, when the polarization state of the input state is not along either |H⟩ or |V⟩ (optical axis of BS) but |D⟩ or |R⟩, the fidelity of the output state is usually worse than that of |H⟩ or |V⟩ input state. The second reason is the imperfect stabilization of the relative phase of UMI which has nearly 4 m-long path length difference. We provide performance test results of our phase stability setup in supplementary note (https://stacks.iop.org/NJP/22/093070/mmedia). We emphasize that non-unity process fidelity is not due to the limitation of our proposed scheme but the imperfection of our experimental demonstration. Further, we remark that this scheme could be uneven weighted superposition of operators via non-50:50 BS while experimental data are focused on equally weighted superposition of operators.

Zoom In Zoom Out Reset image size

Note that in general, a coherent superposition of unitary operators is not a unitary operator. The operator $\frac{1}{\sqrt{2}}\left({\sigma }_{z}\otimes {\sigma }_{z}+{\sigma }_{x}\otimes {\sigma }_{x}\right)$ is composed of unitary operators but it is a non-unitary operator. On the other hand, $\frac{1}{\sqrt{2}}\left(I\otimes I+i{\sigma }_{x}\otimes {\sigma }_{x}\right)$ is a unitary operation. It is known that if U_AB is a two-qubit unitary operation with Schmidt number 2, U_AB has the form of $\sqrt{1-p}I\otimes I+i\sqrt{p}{\sigma }_{x}\otimes {\sigma }_{x}$ up to local unitary equivalence where 0 ⩽ p ⩽ 1 [5]. Hence, one can realize any two-qubit unitary operations with Schmidt number 2 using our scheme. Moreover, it is interesting to consider the possibility of emulating Ising gate, which is a two-qubit gate implemented natively in trapped-ion quantum system, based on our scheme [33, 34]. For example, $\frac{1}{\sqrt{2}}\left(I\otimes I+i{\sigma }_{x}\otimes {\sigma }_{x}\right)$ is exactly the same with 3π/4 Ising (XX) gate [34]. Note that, Ising (XX) gate and single-qubit rotation gates can constitute a universal set of quantum gates.

We emphasize that entangled operations can be extended to the case of M superposed operations ${\mathcal{O}}_{N}^{M}$ for N qubit states by adding optical arms of the interferometers and adding the number of interferometers, respectively, then ${\mathcal{O}}_{N}^{M}$ is given by

$$\begin{equation}{\mathcal{O}}_{N}^{M}=\sum _{k=1}^{M}{c}_{k}{\mathcal{O}}_{k}^{\left(1\right)}\otimes \cdots \otimes {\mathcal{O}}_{k}^{\left(N\right)},\end{equation} \tag{ 5 }$$

where ${\mathcal{O}}_{k}^{\left(j\right)}$ is the kth local operation acting on jth qubit and c_k is the Schmidt coefficient. Note that c_k is adjustable using BS having different reflectivity and transmittivity ratio. Figure 5(a) shows an unbalanced Mach–Zehnder interferometer (UMZI) with four different arms. For an interferometer A, the local operation A_i with i = 0, 1, 2, 3 is located in each arm of the UMZI where the optical path length difference is fixed to L between two neighboring arms and it is the same for the interferometer B. Then, one can prepare an entangled operation with Schmit number 4 of

$$\begin{equation}\frac{1}{2}\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}{\phi }_{1}}\enspace {A}_{2}\otimes {B}_{2}+{\mathrm{e}}^{\mathrm{i}{\phi }_{2}}\enspace {A}_{3}\otimes {B}_{3}+{\mathrm{e}}^{\mathrm{i}{\phi }_{3}}\enspace {A}_{4}\otimes {B}_{4}\right),\end{equation} \tag{ 6 }$$

by post-selecting the case where the arrival time difference of two-photons is zero and ϕ_i with i = 1, 2, 3 is the relative phase differences. In this case, all the other terms are not detected [29, 30]. It is well-known that any two-qubit operation can be decomposed into the form of equation (6) up to local unitary equivalence [35]. Note that we can implement SWAP gate $\frac{1}{2}\left(I\otimes I+{\sigma }_{x}\otimes {\sigma }_{x}+{\sigma }_{y}\otimes {\sigma }_{y}+{\sigma }_{z}\otimes {\sigma }_{z}\right)$ based on the setup shown in figure 5(a). Considering the CNOT complexity of SWAP gate is three [36], i.e., three consecutive CNOT gates are required for a single SWAP gate, it significantly reduces the implementation complexity of SWAP gate.

Zoom In Zoom Out Reset image size

We can also consider increasing the number of qubits by adding more UMZIs as shown in figure 5(b). For example, three photon input states can be prepared by using cascaded SPDC process [37]. In this case, we consider three qubit systems and the corresponding three qubit entangled operation ${\mathcal{O}}_{3}^{M}$ is

$$\begin{equation}{\mathcal{O}}_{3}^{M}=\sum _{k=1}^{M}{c}_{k}{\mathcal{O}}_{k}^{\mathrm{A}}\otimes {\mathcal{O}}_{k}^{\mathrm{B}}\otimes {\mathcal{O}}_{k}^{\mathrm{C}},\end{equation} \tag{ 7 }$$

where ${\mathcal{O}}_{k}^{\mathrm{C}}$ are single qubit operations acting on qubit C. For example, one can obtain three qubit Greenberger–Horne–Zeilinger state [38] $\left\vert GHZ\right\rangle =\frac{1}{\sqrt{2}}\left(\left\vert HHH\right\rangle +\left\vert VVV\right\rangle \right)$ from an input state $\left\vert HHH\right\rangle$ by implementing $\frac{1}{\sqrt{2}}\left(I\otimes I\otimes I+{\sigma }_{x}\otimes {\sigma }_{x}\otimes {\sigma }_{x}\right)$. Likewise, if one implement $\frac{1}{\sqrt{3}}\left(I\otimes I\otimes {\sigma }_{x}+I\otimes {\sigma }_{x}\otimes I+{\sigma }_{x}\otimes I\otimes I\right)$, then one can prepare three qubit W state [39] $\left\vert W\right\rangle =\frac{1}{\sqrt{3}}\left(\left\vert HHV\right\rangle +\left\vert HVH\right\rangle +\left\vert VHH\right\rangle \right)$ from an input state $\left\vert HHH\right\rangle$. Moreover, one can implement the controlled–controlled-unitary (CCU) gate ${\mathcal{O}}_{\text{CCU}}=\vert H\rangle \langle H\vert \otimes \vert H\rangle \langle H\vert \otimes I+\vert H\rangle \langle H\vert \otimes \vert V\rangle \langle V\vert \otimes I+\vert V\rangle \langle V\vert \otimes \vert H\rangle \langle H\vert \otimes I+\vert V\rangle \langle V\vert \otimes \vert V\rangle \langle V\vert \otimes U$. If U = σ_x, then this operation becomes the Toffoli (controlled–controlled NOT) gate [40].

In summary, we have proposed a scheme to implement arbitrary entangled operations based on a coherent superposition of local operations. We also report an experimental demonstration of various two-qubit entangled operations in photonic systems. We believe that our scheme has great importance both in fundamental and practical aspects. Entanglement of operators is closely related to the evolution of quantum systems under nonlocal Hamiltonians and the entangling power of quantum operators [2, 3, 41]. In addition, it is known that superposition of quantum gates cannot be represented by the conventional quantum circuit models [42] and the extended quantum circuit model allowing such superposition of operators can reduce the computational complexity of some problems and simplify realization of various quantum information processing [11, 43]. Due to the simplicity of our scheme and the possibility to extend to multi-qubit systems, it is interesting to apply our scheme to solve practical problems using quantum algorithms such as Hamiltonian simulation [9] and quantum chemistry problem [44]. Moreover, although we mainly discuss unitary operations but the scheme can also be applicable to non-trace-preserving operations. Hence, it is intriguing to consider exploring PT symmetry broken operations [45] and adding a control to weak measurements or partial collapse measurement [46].

We acknowledge funding from KIST institutional program (Project No. 2E30620) and the National Research Foundation of Korea (Grant Nos. 2019M3E4A1079526).

390 nm pulse train is prepared by 1 mm thick LBO crystal via SHG process using a 780 nm mode-locked pump laser (80 MHz repetition rate, 140 fs pulse duration, M² < 1.1, Chameleon, Coherent), and generates photon pairs via type-II SPDC process at a 1 mm thick BBO crystal. The 780 nm pump laser is separated by a DM from 390 nm laser, and used as a locking laser to lock the relative phase between two arms of an UMI. The locking laser enters a one-inch cube BS spatially separated from the single photon's path in order not to be detected at APD. In order to actively lock the relative phase between two arms of UMI from mechanical and thermal vibrations of optical components, we implement a PID control system as shown in figure A1.

Zoom In Zoom Out Reset image size

A.1. Locking the relative phase between two arms of an UMI

We test the performance of our phase locking system using a single balanced Michelson interferometer (MI), meaning that the path length difference between two arms is negligible. Single photon and locking laser are injected to a single balance MI, and the intensity of the locking laser is controlled by driving the voltage to a piezo actuator attached on the mirror of one arm. Then, we measure the single photon count of the signal (down-converted photons) using an APD depending on the intensity of the locking laser. As shown in figure A2(a), we can observe the interference fringes of both signal (black line) and locking laser (red line) at the same time by scanning the mirror on one arm using a piezo actuator (see figure A2(a) after 3600 s). Then, we fixed the intensity of the locking laser around the half of the maximum intensity of the interference fringe by using a PID controller and a voltage amplifier, which enables locking the relative phase between two arms of MI. As shown in figure A2(a), signal is locked to have the minimum count by adjusting the phase using α when intensity of the locking laser is half of the maximum intensity of interference fringe. Figure A2(b) shows the stability of phase locking in the interferometer during an hour, we find that the relative phase on signal is locked. We have considered that the imperfections of our experimental results (purity, concurrence, and fidelity) are mainly due to the phase fluctuation. We implement an entangled operation $\frac{1}{\sqrt{2}}\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {A}_{2}\otimes {B}_{2}\right)$ using a single UMI instead of two UMIs and the results shows the better performance. We will compare this results at the section 3.

Zoom In Zoom Out Reset image size

In order to control the relative phase ϕ of $\frac{1}{\sqrt{2}}\left({A}_{1}\otimes {B}_{1}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {A}_{2}\otimes {B}_{2}\right)$ from 0 to 2π in two UMIs, we use a set of QWP (π/4)–HWP (α)–QWP (π/4) for locking laser on the long arm of the UMI on qubit A, see figure A1. This waveplate combination provides the phase retardation ϕ = 4α + π [47] depending on the HWP's angle α while the polarization is unchanged. Note that, this set of WPs gives a phase shift only for locking laser (not signal). If we give phase difference between two arms of UMI by changing the HWP's angle α, the intensity will be changed according to phase difference from α. However, the optical path length difference is shifted depending on α while keeping the intensity of locking laser at half maximum of the interference fringe using PID control, and it enables a relative phase to be adjustable to any value from 0 to 2π.

A.2. Experimental setup with a single UMI instead of two

In order to confirm that imperfections of our experimental results are mainly from our phase locking system on the UMIs, we realize the same experiment using a single UMI [48, 49] rather than two UMIs as shown in figure A3. Here we send the signal and idler photons into a single BS with a locking laser. Then we can lock the phase of a single UMI instead of two using a single locking laser beam. In this setup, we carry out QST of the output state for the entangled operation $\frac{1}{\sqrt{2}}\left({\sigma }_{z}\otimes {\sigma }_{z}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {\sigma }_{x}\otimes {\sigma }_{x}\right)$ and the results for the input state $\left\vert HH\right\rangle$ is shown in figure A4. We compare the experimental results for two cases: a single UMI and two UMI setups in table A1. By decreasing the number of phase locking from two to one, the experimental results are improved. Purity, fidelity, and concurrence of the output state increase about 0.038, 0.027, and 0.039, respectively. Nevertheless, we have to uses two UMI setup of figure A1 due to the limited spaces for mounting various WPs required to perform QST and QPT. However the comparison summarized in table A1 suggests that reducing number of interferometer can increase the quality of the realized operation. Thus, we believe that our phase locking system have room for improvement.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Table A1. Comparison of experimental results obtained with the setups consisting of either single or double UMIs.

	1 UMI	2 UMIs
Purity	0.942 ± 0.018	0.904 ± 0.025
Fidelity	0.967 ± 0.010	0.940 ± 0.015
Concurrence	0.945 ± 0.017	0.906 ± 0.025

In this section, we provide additional experimental data that are not included in the main text. At first, figure B1 shows the reconstructed output states after applying $1/\sqrt{2}\left({\sigma }_{z}\otimes {\sigma }_{z}+{\mathrm{e}}^{\mathrm{i}\phi }\enspace {\sigma }_{x}\otimes {\sigma }_{x}\right)$ entangled operation and the expected output state is $1/\sqrt{2}\left(\vert HV\rangle +{\mathrm{e}}^{\mathrm{i}\phi }\vert VH\rangle \right)$ for the input state $\left\vert HV\right\rangle$. See figure 3 of the main text for comparison.

Zoom In Zoom Out Reset image size

Furthermore, we perform QPT measurement on $\frac{1}{\sqrt{2}}\left(I\otimes I-{\sigma }_{x}\otimes {\sigma }_{x}\right)$ entangled operation and the experimentally reconstructed process matrix χ_exp is shown in supplementary figure B2. The process fidelity of χ_exp with respect to the ideal operation is 0.830 ± 0.008, which is obtained by performing Monte-Carlo simulations 100 times on the experimental data and the error corresponds to one standard deviation.

Zoom In Zoom Out Reset image size